MLP也被称为人工神经网络(Artificial Neural Network,ANN)的一种基本形式,以下从定义、结构、工作原理、训练算法、应用等方面进行介绍:
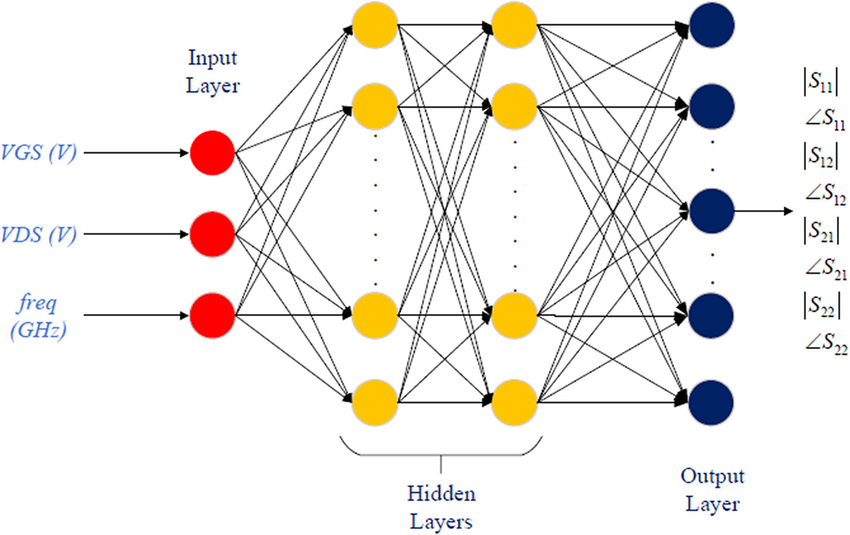
多层感知机是一种前馈人工神经网络,由多个神经元(神经节点)组成,这些神经元按照层次结构排列,包括输入层、隐藏层和输出层,层与层之间的神经元通过权重连接,信息从输入层依次向前传播到输出层,没有反馈连接。
一、结构
1.输入层
- 节点数量:输入层节点数量取决于输入数据的特征维度。比如在MNIST手写数字识别任务中,若输入的是28×28像素的灰度图像,将其展开为一维向量后,输入层节点数量就是28×28=784个。每个节点对应图像中的一个像素值,这些节点负责接收外部输入数据。
- 功能:只是简单地将输入数据传递给下一层,不进行任何计算或处理,其作用是为整个网络提供数据来源。
2.隐藏层
- 层数:隐藏层可以有一层或多层,具体数量根据任务的复杂程度和模型的需求来确定。一般来说,增加隐藏层的数量可以使模型学习到更复杂的特征和模式,但也会增加模型的训练难度和计算量,容易导致过拟合。
- 节点数量:隐藏层节点数量没有固定的标准,通常需要通过实验和调优来确定。一般会随着网络深度的增加而逐渐减少,也可以根据具体问题和经验进行设置,比如常见的有128、256、512等。
- 功能:隐藏层中的神经元对输入数据进行非线性变换和特征提取。每个隐藏层神经元接收上一层神经元的输出,并根据自身的权重和偏置进行加权求和,然后通过激活函数进行非线性处理,将处理后的结果输出给下一层。不同的隐藏层可以学习到不同层次和抽象程度的特征,从原始数据中提取出更有价值的信息,帮助模型更好地进行分类或预测。
3.输出层
- 节点数量:根据任务类型而定。在二分类任务中,输出层通常只有1个节点,输出值可以表示属于某一类别的概率,比如0.8表示属于正类的概率为80%;在多分类任务中,输出层节点数量等于类别数量,例如对10种不同动物进行分类,输出层就有10个节点,每个节点的值表示输入数据属于对应类别的概率或得分。在回归任务中,输出层一般只有一个节点,输出一个连续的数值结果,比如预测房价、股票价格等。
- 功能:根据隐藏层传递过来的信息,在输出层得到最终的预测结果。输出层的输出值通常需要根据具体任务进行解释和处理,例如在分类任务中,通过对输出节点的值进行归一化(如使用Softmax函数),得到属于各个类别的概率分布,然后选择概率最大的类别作为预测结果;在回归任务中,直接将输出节点的值作为预测的数值。
此外,层与层之间的神经元通过权重连接,这些权重在模型训练过程中不断调整和优化,以使得模型能够学习到输入数据和输出目标之间的映射关系。偏置项则用于调整神经元的激活阈值,增加模型的灵活性和表达能力。
二、工作原理
多层感知机(Multilayer Perceptron,MLP)的工作原理主要包括信号的前向传播和误差的反向传播两个过程:
1.前向传播
- 输入层到隐藏层
- 首先,输入数据\\(x=(x_1,x_2,\\cdots,x_n)\\)被传递到输入层,输入层的神经元只是简单地将数据传递给隐藏层。
- 隐藏层的第\\(j\\)个神经元接收输入层的信号,进行加权求和\\(z_j=\\sum_{i = 1}^{n}w_{ij}x_i + b_j\\),其中\\(w_{ij}\\)是输入层第\\(i\\)个神经元到隐藏层第\\(j\\)个神经元的连接权重,\\(b_j\\)是隐藏层第\\(j\\)个神经元的偏置。
- 然后,将加权求和的结果\\(z_j\\)通过激活函数\\(f\\)进行非线性变换,得到隐藏层第\\(j\\)个神经元的输出\\(h_j = f(z_j)\\)。常见的激活函数有Sigmoid函数、ReLU函数等。
- 隐藏层到隐藏层(若有多个隐藏层)
- 对于多个隐藏层的MLP,前一个隐藏层的输出作为下一个隐藏层的输入,重复上述加权求和与激活函数变换的过程。
- 以第\\(l\\)层隐藏层到第\\(l + 1\\)层隐藏层为例,第\\(l + 1\\)层隐藏层的第\\(k\\)个神经元接收第\\(l\\)层隐藏层的输出信号,进行加权求和\\(z_k=\\sum_{j = 1}^{m}w_{jk}h_j + b_k\\),其中\\(w_{jk}\\)是第\\(l\\)层隐藏层第\\(j\\)个神经元到第\\(l + 1\\)层隐藏层第\\(k\\)个神经元的连接权重,\\(b_k\\)是第\\(l + 1\\)层隐藏层第\\(k\\)个神经元的偏置,\\(h_j\\)是第\\(l\\)层隐藏层第\\(j\\)个神经元的输出。
- 再通过激活函数\\(f\\)得到第\\(l + 1\\)层隐藏层第\\(k\\)个神经元的输出\\(h_k = f(z_k)\\)。
- 隐藏层到输出层
- 最后,隐藏层的输出传递到输出层。输出层的神经元同样进行加权求和操作,假设输出层有\\(q\\)个神经元,输出层第\\(r\\)个神经元的输出\\(y_r=\\sum_{k = 1}^{p}w_{kr}h_k + b_r\\),其中\\(w_{kr}\\)是隐藏层第\\(k\\)个神经元到输出层第\\(r\\)个神经元的连接权重,\\(b_r\\)是输出层第\\(r\\)个神经元的偏置,\\(h_k\\)是隐藏层第\\(k\\)个神经元的输出。
- 在分类任务中,通常会对输出层的结果使用Softmax函数进行归一化,得到属于各个类别的概率分布\\(\\hat{y}_r=\\frac{e^{y_r}}{\\sum_{s = 1}^{q}e^{y_s}}\\);在回归任务中,输出层的输出\\(y_r\\)就是最终的预测值。
2.反向传播
- 计算误差
- 在前向传播得到输出结果\\(\\hat{y}\\)后,需要计算预测结果与真实标签\\(y\\)之间的误差。常用的误差函数有均方误差(MSE)、交叉熵损失函数等。以均方误差为例,误差\\(E=\\frac{1}{2}\\sum_{r = 1}^{q}(y_r-\\hat{y}_r)^2\\)。
- 误差反向传播
- 从输出层开始,计算误差对输出层权重和偏置的梯度。以输出层第\\(r\\)个神经元为例,误差对权重\\(w_{kr}\\)的梯度\\(\\frac{\\partial E}{\\partial w_{kr}}=(y_r-\\hat{y}_r)\\hat{y}_r(1-\\hat{y}_r)h_k\\),误差对偏置\\(b_r\\)的梯度\\(\\frac{\\partial E}{\\partial b_r}=(y_r-\\hat{y}_r)\\hat{y}_r(1-\\hat{y}_r)\\)。
- 将误差从输出层反向传播到隐藏层,计算误差对隐藏层权重和偏置的梯度。对于隐藏层第\\(l\\)层的第\\(j\\)个神经元,误差对权重\\(w_{ij}\\)的梯度\\(\\frac{\\partial E}{\\partial w_{ij}}=\\sum_{k}\\frac{\\partial E}{\\partial z_k}\\frac{\\partial z_k}{\\partial w_{ij}}\\),其中\\(\\frac{\\partial E}{\\partial z_k}\\)是误差对第\\(l + 1\\)层隐藏层第\\(k\\)个神经元输入的导数,\\(\\frac{\\partial z_k}{\\partial w_{ij}}=h_j\\)。误差对偏置\\(b_j\\)的梯度\\(\\frac{\\partial E}{\\partial b_j}=\\sum_{k}\\frac{\\partial E}{\\partial z_k}\\frac{\\partial z_k}{\\partial b_j}\\),其中\\(\\frac{\\partial z_k}{\\partial b_j}=1\\)。
- 更新权重和偏置
- 根据计算得到的梯度,使用优化算法(如随机梯度下降SGD、Adagrad、Adadelta、Adam等)来更新权重和偏置。以随机梯度下降为例,权重更新公式为\\(w_{ij}=w_{ij}-\\eta\\frac{\\partial E}{\\partial w_{ij}}\\),偏置更新公式为\\(b_j=b_j-\\eta\\frac{\\partial E}{\\partial b_j}\\),其中\\(\\eta\\)是学习率,控制权重和偏置更新的步长。
通过不断地重复前向传播和反向传播过程,MLP逐渐调整权重和偏置,使得误差不断减小,模型能够学习到输入数据和输出目标之间的映射关系,从而实现对新数据的准确预测和分类等任务。
三、训练算法
- 反向传播算法:是MLP训练的核心算法。在训练过程中,首先进行前向传播得到输出结果,然后根据输出结果与真实标签之间的差异计算损失函数(如均方误差、交叉熵等)。接着,从输出层开始,反向传播损失函数的梯度,计算每一层的权重和偏置的梯度,根据梯度更新权重和偏置,使得损失函数逐渐减小。通过不断重复前向传播和反向传播的过程,调整网络的参数,直到模型收敛或达到预设的训练轮数。
- 优化器:为了更有效地更新权重和偏置,通常会使用各种优化器,如随机梯度下降(SGD)及其变种Adagrad、Adadelta、Adam等。这些优化器可以根据不同的情况自适应地调整学习率,加快模型的收敛速度,提高训练效率和稳定性。
四、应用案例
1.计算机视觉领域
将图像的像素值作为输入,通过多层感知机学习图像的特征,实现对图像的分类,如识别手写数字、区分不同种类的动物等。
- MNIST手写数字识别:在MNIST数据集上,MLP可以将手写数字的图像像素值作为输入,经过多个隐藏层对图像特征进行学习和提取,在输出层输出对应数字的类别概率,从而准确识别出0-9的手写数字。
- 人脸识别:将人脸图像的特征向量作为输入,MLP通过学习不同人脸的特征模式,能够在输出层判断输入图像是否属于特定的人,或者对不同的人脸进行分类识别。
2.自然语言处理领域
- 垃圾邮件检测:把邮件文本内容进行向量化表示后输入MLP,MLP通过学习垃圾邮件和正常邮件的文本特征,在输出层输出该邮件是垃圾邮件或正常邮件的概率,实现对邮件的分类。
- 命名实体识别:对输入的文本序列进行处理,MLP可以学习文本中不同词汇的上下文特征等,识别出文本中的人名、地名、组织机构名等命名实体。
- 语音识别:把语音信号的特征作为输入,经过MLP处理后将语音转换为文字,或者进行语音命令的识别和分类。
3.推荐系统领域
- 视频推荐:以用户的历史观看记录、点赞收藏行为、搜索关键词等数据作为输入,MLP学习用户的兴趣偏好,在输出层为用户推荐可能感兴趣的视频内容,帮助视频平台提高用户的观看时长和活跃度。
- 商品推荐:分析用户的购买历史、浏览行为、商品评价等数据,MLP可以挖掘用户的潜在需求,向用户推荐符合其喜好的商品,提高电商平台的销售额和用户满意度。
4.金融领域
- 股票价格预测:将历史股票价格、成交量、宏观经济数据、公司财务数据等作为输入特征,MLP通过学习这些数据与股票价格之间的非线性关系,在输出层预测未来的股票价格走势,为投资者提供决策参考。
- 信用卡风险评估:以用户的年龄、收入、信用记录、消费行为等数据作为输入,MLP评估用户使用信用卡时的违约风险,输出用户的风险等级,帮助银行制定合理的信用卡额度和风险管理策略。
5.医疗健康领域
- 疾病诊断:把患者的症状表现、检查检验结果、病史等数据输入MLP,MLP学习这些数据与疾病之间的关联,在输出层辅助医生判断患者可能患有的疾病,提高诊断的准确性和效率。
- 药物研发:根据药物的化学结构、靶点信息、生物活性数据等,MLP可以预测药物的疗效、毒性等性质,帮助研究人员筛选出有潜力的药物分子,加速药物研发进程。
6.工业制造领域
- 产品质量检测:在生产线上,将产品的外观特征、尺寸参数、性能指标等数据作为输入,MLP学习合格产品和不合格产品的特征差异,在输出层判断产品是否合格,及时发现生产过程中的质量问题。
- 设备故障预测:以设备的运行参数、振动数据、温度变化等作为输入,MLP通过学习设备正常运行和故障状态下的数据特征,提前预测设备可能出现的故障,以便安排预防性维护,减少设备停机时间。