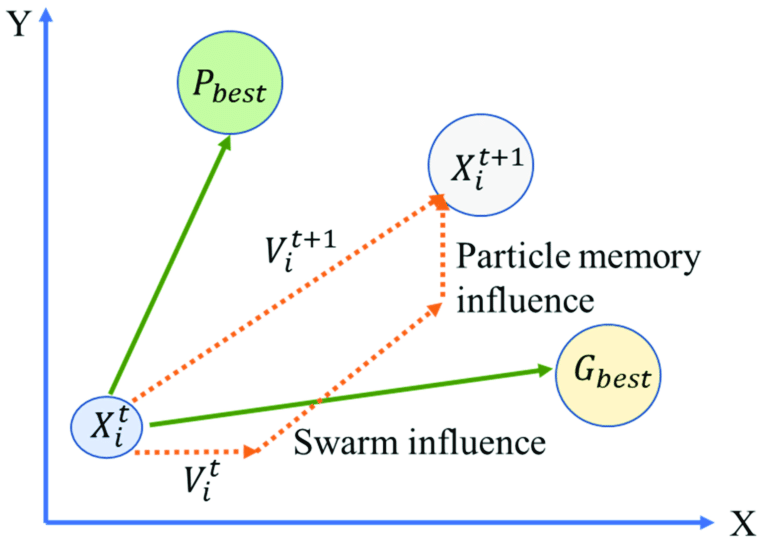
粒子群优化(Particle Swarm Optimization, PSO)是一种基于群体智能的优化算法,由Eberhart和Kennedy在1995年提出。它受到鸟群觅食行为的启发,通过模拟鸟群或鱼群等生物群体的社会行为来进行问题求解。
PSO算法是由James Kennedy和Russell Eberhart在1995年首次提出的。它的灵感来源于对鸟群捕食行为的观察,特别是飞鸟集群活动的规律性。
在PSO算法的早期版本中,引入了惯性权重(w)来更好地控制算法的探索(exploration)和开发(exploitation)。这形成了PSO的标准版本。
为了提高PSO算法的性能和实用性,学术界对其进行了进一步的研究和改进。例如,中山大学和格拉斯哥大学等机构开发了自适应(Adaptive PSO)版本和离散(discrete)版本。
PSO算法因其易于理解和实现、全局搜索能力强等特点,受到了科学与工程领域的广泛关注。
一、基本概念:
1. 粒子(Particle):在PSO中,每个解被视为搜索空间中的一个“粒子”,代表问题的潜在解。
2. 速度(Velocity):每个粒子都有一个速度,决定了它在搜索空间中的移动方向和速度。
3. 位置(Position):粒子在搜索空间中的位置,代表了问题的当前解。
4. 个体最优(pBest):每个粒子所找到的最优解,即该粒子历史上所达到的最优位置。
5. 全局最优(gBest):整个粒子群中所有粒子所找到的最优解,即所有粒子的个体最优中最好的一个。
6. 惯性权重(Inertia Weight):控制粒子保持当前运动方向的程度,较高的惯性权重可以使粒子在搜索空间中探索得更远,而较低的惯性权重有助于粒子在找到好解后快速收敛。
7. 学习因子(Learning Factors):通常有两个学习因子\\( c_1 \\)和\\( c_2 \\),它们决定了粒子向个体最优和全局最优位置移动的强度。
二、算法步骤:
1. 初始化:随机初始化一群粒子的位置和速度。
2. 评价:计算每个粒子的适应度值,即它们所代表的解的质量。
3. 更新个体最优:如果当前粒子的适应度比个体最优的适应度好,则更新个体最优。
4. 更新全局最优:如果当前粒子的适应度比全局最优的适应度好,则更新全局最优。
5. 更新速度和位置:根据个体最优和全局最优更新每个粒子的速度和位置。
6. 迭代:重复步骤2-5,直到满足停止条件,如达到最大迭代次数或解的质量达到预设阈值。
三、应用场景
以下是一些典型的PSO应用场景:
1. 函数优化:PSO可以用于寻找复杂函数的全局最优解,这在工程、经济学、金融等领域的参数优化问题中非常有用。
2. 神经网络训练:PSO可用于优化神经网络的权重和结构参数,提高学习性能和分类精度。
3. 模式识别:在模式识别领域,PSO可以用于特征选择和分类器参数优化,提高分类准确率。
4. 机器学习:PSO在机器学习中用于模型参数优化、特征权重学习等任务,提升模型性能。
5. 控制系统优化:在自动控制领域,PSO可以用于优化控制策略和控制器参数,增强系统的稳定性和响应性能。
6. 路径规划:例如在旅行商问题(TSP)中,PSO可以用来找到最短或最优路径。
7. 调度问题:在生产调度、交通调度等场景中,PSO用于求解资源分配和时间安排的优化问题。
8. 结构优化:在土木工程和机械设计中,PSO可以用于结构设计参数优化,以达到减轻重量或增加强度的目的。
9. 经济学和金融:PSO在投资组合优化、风险管理等方面有应用,帮助找到最优投资策略。
10. 信号处理:在信号处理领域,PSO可以用于滤波器设计、图像处理等参数优化问题。
11. 电力系统:PSO在电力系统的经济调度、电网优化等方面有应用,提高能源利用效率。
12. 水资源管理:在水资源分配和管理问题中,PSO可以用于优化水资源的分配方案。
13. 带约束优化问题:PSO也可以应用于带有约束条件的优化问题,通过适当的修改来满足特定约束。
粒子群优化算法的这些应用场景展示了其在解决实际问题中的灵活性和有效性。随着研究的深入和技术的发展,PSO的应用领域还在不断扩展。
四、优缺点
粒子群优化(PSO)算法作为一种基于群体智能的优化算法,具有以下优缺点:
### 优点:
1. 简单易实现:PSO算法的原理相对简单,易于理解和实现。
2. 全局搜索能力强:PSO算法具有较好的全局搜索能力,能够在搜索空间中找到较好的解。
3. 参数设置少:PSO算法需要设置的参数较少,降低了调参的难度。
4. 适应性强:PSO算法适用于连续优化问题和离散优化问题,可以应用于多种领域。
5. 并行处理:由于每个粒子的更新独立于其他粒子,PSO天然支持并行计算。
6. 自适应性:通过调整参数,如惯性权重、学习因子等,PSO可以适应不同复杂度和规模的问题。
### 缺点:
1. 早熟收敛:PSO算法在迭代过程中容易过早收敛至局部最优解,导致无法找到全局最优解。
2. 参数敏感性:虽然参数较少,但它们对算法性能影响较大,参数选择不当可能导致搜索效率降低或无法收敛。
3. 迭代次数需求:PSO算法通常需要较多的迭代次数才能达到较好的结果,计算时间较长。
4. 局部搜索能力不足:尽管全局搜索能力强,但对于需要精细局部优化的问题,PSO可能不如局部搜索算法高效。
5. 随机性:算法高度依赖于初始值和每次迭代中的随机扰动,可能导致结果的重复性较差。
6. 对解空间分布敏感:如果解空间分布不均匀,可能会导致搜索效率低下。
针对这些缺点,研究者们提出了多种改进的PSO算法,如添加收敛因子、惯性权重模型、粒子群混合算法等,以提高算法性能和适用性。
五、Python应用
粒子群优化(PSO)算法在Python中的实现相对简单,以下是一个基本的PSO算法的Python样例代码。这个例子演示了如何使用Python实现一个简单的PSO算法来寻找一个一维函数的最优解。
```python
import numpy as np
import random
# 定义目标函数,这里以一个简单的二次函数为例
def objective_function(x):
return x2
# 初始化粒子群
def initialize_swarm(size, dimensions):
particles = []
for _ in range(size):
particle = {
'position': np.random.uniform(-10, 10, dimensions),
'velocity': np.random.uniform(-1, 1, dimensions),
'best_position': np.array([None] dimensions),
'best_fitness': float('inf')
}
particles.append(particle)
return particles
# 评估粒子适应度
def evaluate_fitness(particles):
fitness_scores = []
for particle in particles:
fitness = objective_function(particle['position'])
fitness_scores.append(fitness)
if fitness < particle['best_fitness']:
particle['best_fitness'] = fitness
particle['best_position'] = particle['position'].copy()
return np.array(fitness_scores)
# 更新粒子位置和速度
def update_particles(particles, w=0.7, c1=1.5, c2=1.5):
global best_position
global best_fitness
for particle in particles:
fitness = evaluate_fitness(particle)
if fitness < best_fitness:
best_fitness = fitness
best_position = particle['position'].copy()
r1, r2 = random.random(), random.random()
for i in range(len(particle['position'])):
particle['velocity'][i] = w particle['velocity'][i] + \\
c1 r1 (particle['best_position'][i] - particle['position'][i]) + \\
c2 r2 (best_position[i] - particle['position'][i])
particle['position'][i] += particle['velocity'][i]
# 主函数
def main():
global best_position
global best_fitness
best_position = np.array([None])
best_fitness = float('inf')
swarm_size = 30
dimensions = 1
max_iter = 100
particles = initialize_swarm(swarm_size, dimensions)
for _ in range(max_iter):
update_particles(particles)
print(f\"Best position: {best_position}\")
print(f\"Best fitness: {best_fitness}\")
if __name__ == \"__main__\":
main()
```
这段代码首先定义了一个目标函数,然后初始化了一个粒子群,并在每次迭代中评估每个粒子的适应度,更新粒子的位置和速度。粒子群中的每个粒子都试图找到目标函数的最小值。最终,算法输出找到的最优解和对应的适应度值。
这个例子是非常基础的,实际应用中可能需要根据问题的特性调整参数,如惯性权重(w)、个体学习因子(c1)和群体学习因子(c2),以及粒子群的大小和迭代次数等。
PSO算法以其简单性、易实现性和高效性在许多领域得到了广泛应用,包括函数优化、神经网络训练、模式识别等。然而,它也有一些局限性,比如可能会陷入局部最优,或者在某些情况下收敛速度较慢。为了解决这些问题,研究者们提出了许多改进的PSO算法。