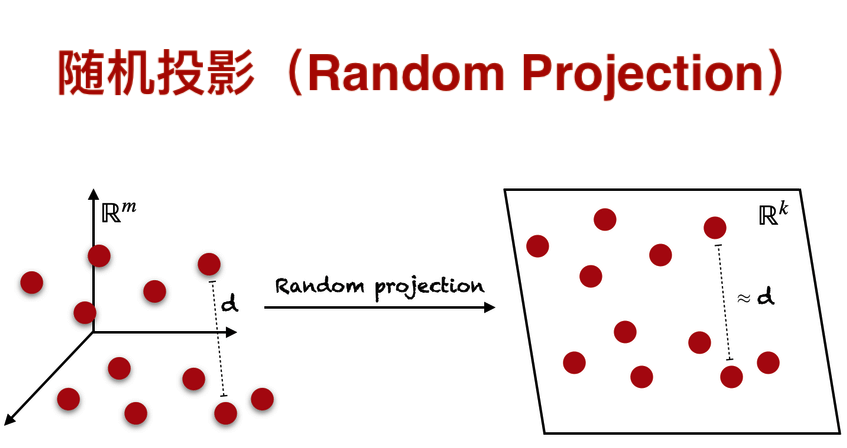
随机投影(Random Projection)是一种在数据挖掘和机器学习中常用的技术,它通过将高维数据映射到低维空间来减少数据的维度,同时尽可能地保留原始数据的结构。这种方法在处理大规模数据集时特别有用,因为它可以显著减少计算和存储需求。
一、基本原理
随机投影的基本思想是使用一个随机生成的矩阵来将原始数据投影到一个较低维度的空间。这个随机矩阵的行数是目标维度,而列数是原始数据的维度。通过乘以这个矩阵,原始数据的每一行都会映射到一个较短的向量上。
二、算法步骤
1. **选择目标维度**:确定你希望将数据投影到的维度,这通常远小于原始数据的维度。
2. **生成随机矩阵**:创建一个大小为 d ✕ n 的随机矩阵,其中 d 是目标维度,n 是原始数据的维度。
3. **矩阵乘法**:将原始数据集(通常是一个 m ✕ n 的矩阵,m 是样本数)与随机矩阵相乘,得到投影后的数据集。
三、重要性质
- **Johnson-Lindenstrauss 引理**:这是随机投影算法的理论基础,它保证了在一定条件下,高维数据集通过随机投影到低维空间后,任意两点之间的距离几乎保持不变。
- **空间效率**:由于目标维度远小于原始维度,因此随机投影可以显著减少数据存储的需求。
- **时间效率**:随机矩阵的生成和矩阵乘法都是快速操作,这使得随机投影在处理大数据集时非常高效。
四、应用场景
1. **大规模数据处理**:在商业智能和数据挖掘中,处理大规模数据集是一个常见需求。随机投影可以有效地降低数据的维度,通过随机投影减少数据的体积从而减少存储需求和提高数据处理速度。
2. **机器学习模型训练**:在训练机器学习模型时,高维特征空间可能会导致计算成本高昂。通过使用随机投影降低特征空间的维度,可以加快模型的训练过程,同时保持模型的性能。
3. **推荐系统**:在推荐系统中,用户和产品通常由高维特征向量表示。随机投影可以用于减少特征空间的维度,从而提高推荐算法的效率和准确性。
4. **计算机视觉**:在图像处理和识别任务中,图像数据通常具有高维度。随机投影可以用于降低图像数据的维度,以加速图像搜索和分类算法。
5. **隐私保护**:在需要保护用户隐私的应用中,随机投影可以作为一种匿名化技术,通过降低数据的维度来隐藏敏感信息,同时保留数据的有用特征。
6. **金融风险管理**:在金融领域,随机投影可以用于降低风险模型的维度,以便快速识别和评估潜在的风险因素。
7. **供应链优化**:在供应链管理中,随机投影可以帮助企业通过降低库存数据的维度来优化库存管理,提高物流效率。
8. **广告投放**:在线广告投放平台可以利用随机投影技术来分析用户行为数据,降低数据处理的复杂性,并提高广告投放的精准度。
9. **搜索引擎优化**:搜索引擎可以利用随机投影来改进排名算法,通过降低搜索空间的维度来提高搜索结果的相关性。
10. **随机投影神经网络(RPNN)**:在某些情况下,商业应用可能需要快速且稳定的数值分析解决方案。RPNN提供了一种具有预定和固定内部权重和偏差的ANN,可以显著减少训练时间,同时保持较高的精度[^7^]。
通过这些应用案例,我们可以看到随机投影技术在商业领域的多样性和实用性。它不仅能够提高数据处理的效率,还能够在保持数据特征的同时降低计算成本。
五、缺点
- **信息损失**:由于数据被投影到更低维度的空间,一些信息可能会丢失。
- **随机性**:结果依赖于随机矩阵的生成,这可能导致不同的运行结果不同。
六、Python实现
在Python中,实现随机投影算法通常使用`numpy`库,它提供了强大的多维数组对象以及对这些数组进行操作的函数。以下是使用`numpy`实现随机投影的一个简单示例:
```python
import numpy as np
def random_projection(data, target_dim):
\"\"\"
对数据进行随机投影以降低维度。
参数:
data -- 输入数据,形状为 (m, n) 的二维numpy数组,其中 m 是样本数,n 是特征数。
target_dim -- 投影后的数据维度。
返回:
projected_data -- 投影后的数据,形状为 (m, target_dim) 的二维numpy数组。
\"\"\"
# 原始数据的维度
original_dim = data.shape[1]
# 生成一个随机矩阵,其形状为 (target_dim, original_dim)
# 随机矩阵的每个元素都是从标准正态分布中抽取的
random_matrix = np.random.randn(target_dim, original_dim)
# 使用随机矩阵对原始数据进行投影
projected_data = np.dot(data, random_matrix)
return projected_data
# 示例
if __name__ == \"__main__\":
# 创建一个示例数据集,例如 100 个样本,每个样本有 50 个特征
data = np.random.rand(100, 50)
# 将数据投影到 10 维空间
projected_data = random_projection(data, 10)
# 打印投影后的数据形状
print(\"Projected data shape:\", projected_data.shape)
```
在这个示例中,`random_projection`函数接受两个参数:`data`是原始数据集,`target_dim`是投影后的目标维度。函数内部首先计算原始数据的特征数,然后生成一个形状为`(target_dim, original_dim)`的随机矩阵。这个矩阵的每个元素都是从标准正态分布中随机抽取的。然后,使用`numpy`的`dot`函数将原始数据与随机矩阵相乘,得到投影后的数据。
请注意,这个示例仅用于演示随机投影的基本思想,实际应用中可能需要根据具体情况进行调整。此外,随机投影的效果很大程度上取决于随机矩阵的生成,因此在不同的运行中可能会得到不同的结果。
随机投影是一种简单而强大的工具,它在处理高维数据时提供了一种有效的方法来减少数据的复杂性,同时保持数据的有用特性。