在数据分析工作中,“数据打架”是常见难题——当身高以“厘米”为单位、体重以“千克”为单位同时进入模型时,数值范围的差异会严重干扰分析结果。Z-score标准化正是解决这一问题的核心工具,它能将不同量级的数据转化为统一尺度,为后续分析扫清障碍。
一、Z-score标准化的定义
1.标准定义
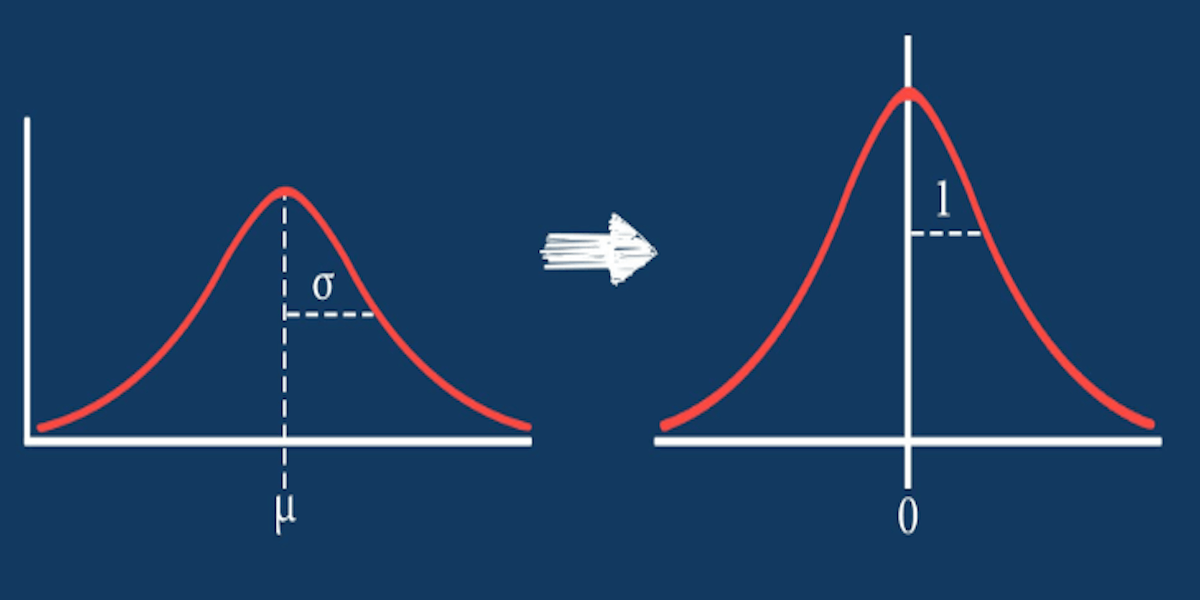
Z-score标准化(Standard Score Normalization),又称标准差标准化或Z值标准化,是一种将原始数据转换为均值为0、标准差为1的标准化数据的统计方法。通过该方法处理后的数据(即Z值),能够直观反映原始数据在整体数据分布中的相对位置,有效消除不同变量间的量纲和量级差异,使多维度数据具备可比较性。
2.核心计算公式
其计算公式为:Z = (X - μ) / σ,其中X代表原始数据,μ是数据样本的均值,σ是样本的标准差。简单来说,Z值本质上反映了原始数据与样本均值的偏离程度,以标准差为“尺子”量化这种偏离,正Z值表示数据高于均值,负Z值则表示低于均值。
3.实例计算过程
结合具体实例能更清晰理解计算逻辑。假设某班级10名学生的数学成绩为:85、92、78、90、88、95、72、83、89、91。计算步骤如下:
第一步,计算样本均值μ:μ = (85+92+78+90+88+95+72+83+89+91)/10 = 86.5;
第二步,计算样本标准差σ:先求各数据与均值差的平方和,即(85-86.5)²+(92-86.5)²+…+(91-86.5)² = 346.5,再计算方差为346.5/10 = 34.65,最终标准差σ≈5.886;
第三步,计算Z值:以成绩85为例,其Z值为(85-86.5)/5.886≈-0.255,说明该成绩略低于均值,偏离程度较小。
二、Z-score标准化的适用场景与实践案例
1.核心适用场景
Z-score标准化的适用场景具有鲜明特征,主要集中在以下两类场景:
一是数据近似服从正态分布,或后续分析对数据分布有正态性要求的场景。例如在回归分析、主成分分析、聚类分析等算法中,它能确保各变量权重平等,避免因量级差异导致的分析偏差;
二是异常值识别场景。通常认为|Z|>3的数值属于极端异常值,可作为数据清洗的重要依据,帮助筛选出不符合常规的数据点。
需特别注意的是,若数据存在严重偏态或异常值过多,Z-score标准化的效果会大打折扣,此时需先处理数据分布问题或选择其他标准化方法。
2.实践案例:智能鞋垫传感器数据标准化
在智能健康监测领域,智能鞋垫常嵌入压力传感器、加速度传感器和心率传感器,用于采集用户行走时的多维度数据,以评估步态健康状况。采集的核心数据包括足底压力(单位:千帕,范围50-500kPa)、步频(单位:步/分钟,范围60-120步/分)及足底接触时间(单位:毫秒,范围200-500ms)。
由于这些数据的量纲和数值范围差异极大,直接输入步态分析模型会导致“足底压力”因数值量级大而占据主导地位,掩盖步频、接触时间等关键特征的影响。此时采用Z-score标准化处理,可有效解决这一问题。
例如,某用户的一组原始数据为:足底压力320kPa(样本均值μ₁=280kPa,标准差σ₁=60kPa)、步频95步/分(样本均值μ₂=85步/分,标准差σ₂=10步/分)、接触时间320ms(样本均值μ₃=350ms,标准差σ₃=30ms)。经计算,其Z值分别为(320-280)/60≈0.667、(95-85)/10=1、(320-350)/30=-1。标准化后的数据消除了量纲干扰,模型可平等捕捉三类特征的变化,进而精准识别如“足底压力分布不均”“步频异常”等步态问题,为运动损伤预警或康复评估提供可靠依据。
三、Z-score标准化的特性与实现方式
1.核心优势与局限性
Z-score标准化的优势十分突出:一是计算简便,无需复杂的参数设定;二是能保留原始数据的分布特征和相对关系,不改变数据的内在规律;三是可通过Z值直接判断数据位置,便于异常值识别。
但缺点也不容忽视:首先,它对数据分布和极端值敏感,若原始数据中存在极大或极小值,会直接影响均值和标准差的准确性,导致标准化结果失真;其次,其结果会出现正负值,不适用于要求非负数据的场景,如图像识别中的像素值处理。
2.与其他标准化方法的对比
与主流标准化方法相比,Z-score标准化的定位明确:
与min-max标准化(归一化)相比,min-max将数据压缩至[0,1]区间,对异常值更敏感,适用于非负数据场景;而Z-score输出范围无限制,更适合正态分布数据和需要保留数据偏离信息的场景。
与小数定标标准化相比,Z-score无需人工设定缩放倍数,自动化程度更高,但通用性稍逊于前者,对数据分布的要求更严格。
3.常用编程语言实现函数
在实际数据分析中,无需手动计算Z值,主流编程语言的第三方库均提供了高效的Z-score标准化工具,以下为常用实现方式:
(1)Python(基于scikit-learn库)
scikit-learn的preprocessing模块中StandardScaler类是实现Z-score标准化的常用工具,其底层会自动计算数据的均值和标准差并完成转换,支持批量数据处理,且可与后续建模流程无缝衔接。
Plain Text
from sklearn.preprocessing import StandardScaler
import numpy as np
# 构造示例数据(如智能鞋垫的3个特征数据,每行代表1个样本)
data = np.array([[320, 95, 320], [280, 85, 350], [350, 100, 290], [250, 70, 380]])
# 初始化标准化器
scaler = StandardScaler()
# 执行标准化(fit计算均值和标准差,transform完成转换)
data_zscore = scaler.fit_transform(data)
# 输出结果(均值接近0,标准差接近1)
print(\"标准化后数据:\")
print(data_zscore)
print(\"各特征均值:\", scaler.mean_)
print(\"各特征标准差:\", scaler.scale_)
(2)Python(基于pandas库)
pandas库的mean()和std()方法可直接计算均值和标准差,通过公式手动实现标准化,灵活性更高,适合小批量数据或需自定义逻辑的场景。
Plain Text
import pandas as pd
# 构造DataFrame格式数据
df = pd.DataFrame({
\"足底压力(kPa)\": [320, 280, 350, 250],
\"步频(步/分)\": [95, 85, 100, 70],
\"接触时间(ms)\": [320, 350, 290, 380]
})
# 按列(特征)执行Z-score标准化
df_zscore = (df - df.mean()) / df.std()
print(\"标准化后数据:\")
print(df_zscore)
(3)R语言
R语言的scale()函数是内置的Z-score标准化工具,默认按列处理数据,返回标准化后的矩阵,使用简洁高效。
Plain Text
# 构造示例数据
data <- matrix(c(320, 280, 350, 250, 95, 85, 100, 70, 320, 350, 290, 380),
ncol = 3,
dimnames = list(NULL, c(\"足底压力(kPa)\", \"步频(步/分)\", \"接触时间(ms)\")))
# 执行Z-score标准化
data_zscore <- scale(data)
# 输出结果
cat(\"标准化后数据:\\n\")
print(data_zscore)
cat(\"各特征均值:\", colMeans(data_zscore), \"\\n\") # 接近0
cat(\"各特征标准差:\", apply(data_zscore, 2, sd), \"\\n\") # 接近1
四、总结:Z-score标准化的核心价值
作为数据分析的基础工具,Z-score标准化的核心价值在于构建“数据共通语言”。它打破了不同量纲数据间的壁垒,让多维度特征能够在同一尺度下被分析和利用。掌握其原理、适用场景及计算方法,能帮助数据从业者在特征工程环节做出更合理的选择,为后续建模分析筑牢基础,让数据真正发挥其价值。
在数据分析工作中,“数据打架”是常见难题——当身高以“厘米”为单位、体重以“千克”为单位同时进入模型时,数值范围的差异会严重干扰分析结果。Z-score标准化正是解决这一问题的核心工具,它能将不同量级的数据转化为统一尺度,为后续分析扫清障碍。
标准定义:Z-score标准化(Standard Score Normalization),又称标准差标准化或Z值标准化,是一种将原始数据转换为均值为0、标准差为1的标准化数据的统计方法。通过该方法处理后的数据(即Z值),能够直观反映原始数据在整体数据分布中的相对位置,有效消除不同变量间的量纲和量级差异,使多维度数据具备可比较性。
其计算公式为:Z = (X - μ) / σ,其中X代表原始数据,μ是数据样本的均值,σ是样本的标准差。简单来说,Z值本质上反映了原始数据与样本均值的偏离程度,以标准差为“尺子”量化这种偏离,正Z值表示数据高于均值,负Z值则表示低于均值。
这种方法的适用场景具有鲜明特征。当数据近似服从正态分布,或后续分析对数据分布有正态性要求时,Z-score标准化是最优选择,例如在回归分析、主成分分析、聚类分析等算法中,它能确保各变量权重平等。此外,当需要识别异常值时,Z-score也能发挥作用——通常认为|Z|>3的数值属于极端异常值,可作为数据清洗的重要依据。但需注意,若数据存在严重偏态或异常值过多,其效果会大打折扣。
应用场景案例:智能鞋垫传感器数据标准化:在智能健康监测领域,智能鞋垫常嵌入压力传感器、加速度传感器和心率传感器,用于采集用户行走时的足底压力(单位:千帕,范围50-500kPa)、步频(单位:步/分钟,范围60-120步/分)及足底接触时间(单位:毫秒,范围200-500ms)等多维度数据,以评估步态健康状况。由于这些数据的量纲和数值范围差异极大,直接输入步态分析模型会导致“足底压力”因数值量级大而占据主导地位,掩盖步频、接触时间等关键特征的影响。
此时采用Z-score标准化处理,可将三类数据统一转换为均值为0、标准差为1的标准数据。例如,某用户的一组原始数据为:足底压力320kPa(样本均值μ₁=280kPa,标准差σ₁=60kPa)、步频95步/分(样本均值μ₂=85步/分,标准差σ₂=10步/分)、接触时间320ms(样本均值μ₃=350ms,标准差σ₃=30ms)。经计算,其Z值分别为(320-280)/60≈0.667、(95-85)/10=1、(320-350)/30=-1。标准化后的数据消除了量纲干扰,模型可平等捕捉三类特征的变化,进而精准识别如“足底压力分布不均”“步频异常”等步态问题,为运动损伤预警或康复评估提供可靠依据。
结合实例能更清晰理解计算过程。假设某班级10名学生的数学成绩为:85、92、78、90、88、95、72、83、89、91。首先计算均值μ = (85+92+78+90+88+95+72+83+89+91)/10 = 86.5。再计算标准差σ,先求各数据与均值差的平方和:(85-86.5)²+(92-86.5)²+…+(91-86.5)² = 346.5,方差为346.5/10 = 34.65,标准差σ≈5.886。以成绩85为例,其Z值为(85-86.5)/5.886≈-0.255,说明该成绩略低于均值,偏离程度较小。
Z-score标准化的优势十分突出:计算简便,能保留原始数据的分布特征和相对关系,且可通过Z值直接判断数据位置。但缺点也不容忽视,它对数据分布和极端值敏感,若原始数据中存在极大或极小值,会直接影响均值和标准差的准确性,导致标准化结果失真。同时,其结果会出现正负值,不适用于要求非负数据的场景,如图像识别中的像素值处理。
与其他标准化方法相比,Z-score与min-max标准化(归一化)差异显著。min-max将数据压缩至[0,1]区间,对异常值更敏感,适用于非负数据场景;而Z-score输出范围无限制,更适合正态分布数据和需要保留数据偏离信息的场景。与小数定标标准化相比,Z-score无需人工设定缩放倍数,自动化程度更高,但通用性稍逊于前者。
常用编程语言实现函数:在实际数据分析中,无需手动计算Z值,主流编程语言的第三方库均提供了高效的Z-score标准化工具,以下为常用实现方式:
1.Python(基于scikit-learn库):scikit-learn的preprocessing模块中StandardScaler类是实现Z-score标准化的常用工具,其底层会自动计算数据的均值和标准差并完成转换,支持批量数据处理,且可与后续建模流程无缝衔接。
python
from sklearn.preprocessing import StandardScaler
import numpy as np
# 构造示例数据(如智能鞋垫的3个特征数据,每行代表1个样本)
data = np.array([[320, 95, 320], [280, 85, 350], [350, 100, 290], [250, 70, 380]])
# 初始化标准化器
scaler = StandardScaler()
# 执行标准化(fit计算均值和标准差,transform完成转换)
data_zscore = scaler.fit_transform(data)
# 输出结果(均值接近0,标准差接近1)
print(\"标准化后数据:\")
print(data_zscore)
print(\"各特征均值:\", scaler.mean_)
print(\"各特征标准差:\", scaler.scale_)
2.Python(基于pandas库):pandas库的mean()和std()方法可直接计算均值和标准差,通过公式手动实现标准化,灵活性更高,适合小批量数据或需自定义逻辑的场景。
python
import pandas as pd
# 构造DataFrame格式数据
df = pd.DataFrame({
\"足底压力(kPa)\": [320, 280, 350, 250],
\"步频(步/分)\": [95, 85, 100, 70],
\"接触时间(ms)\": [320, 350, 290, 380]
})
# 按列(特征)执行Z-score标准化
df_zscore = (df - df.mean()) / df.std()
print(\"标准化后数据:\")
print(df_zscore)
3.R语言:R语言的scale()函数是内置的Z-score标准化工具,默认按列处理数据,返回标准化后的矩阵,使用简洁高效。
r
# 构造示例数据
data <- matrix(c(320, 280, 350, 250, 95, 85, 100, 70, 320, 350, 290, 380),
ncol = 3,
dimnames = list(NULL, c(\"足底压力(kPa)\", \"步频(步/分)\", \"接触时间(ms)\")))
# 执行Z-score标准化
data_zscore <- scale(data)
# 输出结果
cat(\"标准化后数据:\\n\")
print(data_zscore)
cat(\"各特征均值:\", colMeans(data_zscore), \"\\n\") # 接近0
cat(\"各特征标准差:\", apply(data_zscore, 2, sd), \"\\n\") # 接近1
作为数据分析的基础工具,Z-score标准化的核心价值在于构建“数据共通语言”。掌握其原理、适用场景及计算方法,能帮助数据从业者在特征工程环节做出更合理的选择,为后续建模分析筑牢基础,让数据真正发挥其价值。