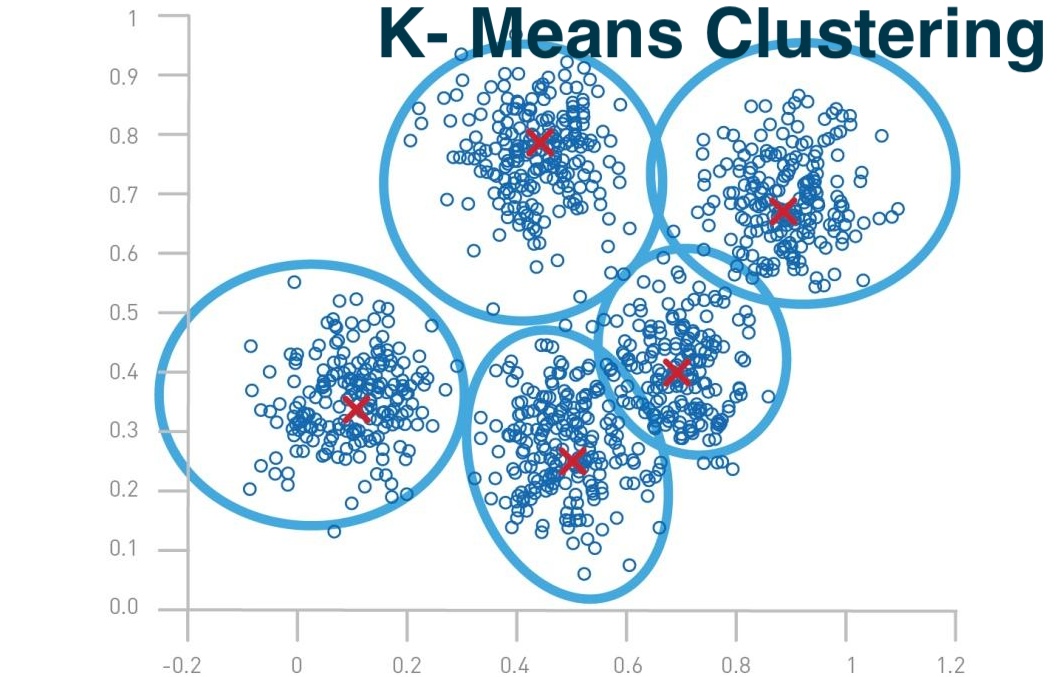
K-均值聚类 (K-Means Clustering)是一种经典的无监督学习算法,用于将数据集分成K个不同的簇。其核心思想是将数据点根据距离的远近分配到不同的簇中,使得簇内的点尽可能相似,簇间的点尽可能不同。
一、商业领域的多种应用场景
1. **客户细分**:在市场营销领域,K-均值聚类可以用于客户细分,将客户根据购买行为、偏好等特征划分为不同的群体。这有助于企业更好地理解客户需求,制定个性化的营销策略,提高客户满意度和忠诚度。
2. **产品推荐**:基于K-均值聚类的客户分群结果,企业可以为不同群体的客户提供个性化的产品推荐,增强购买意愿和转化率。
3. **图像处理**:在图像分析领域,K-均值聚类可以用于图像分割和颜色量化,帮助识别图像中的不同区域或对象,以及减少图像颜色数量以优化存储和传输。
4. **文本挖掘**:K-均值聚类应用于文本挖掘,可以进行文档聚类,将内容相似的文档归为一类,以及主题识别,从文档集合中发现主要话题和模式。
5. **生物信息学**:在生物信息学领域,该算法可用于基因表达数据的聚类,发现具有相似表达模式的基因群体,有助于理解基因功能和生物过程。
6. **异常检测**:K-均值聚类还可以用于识别数据中的异常或离群点,例如在信用卡欺诈检测或网络安全中识别异常行为。
7. **供应链优化**:通过客户和产品的销售数据聚类,优化库存管理和供应链效率,减少库存成本。
8. **风险管理**:在金融行业,K-均值聚类可以帮助识别风险模式,比如通过交易行为分析来识别潜在的欺诈风险。
9. **广告投放**:通过分析用户的行为和偏好,K-均值聚类可以用于精准定位广告投放,提高广告效率和投资回报率。
10. **市场趋势分析**:企业可以利用K-均值聚类分析市场趋势,识别新兴市场机会和潜在的增长点。
K-均值聚类算法的商业应用非常广泛,它通过无监督学习的方式揭示数据内在结构,为决策者提供有价值的洞察。然而,需要注意的是,K-均值聚类算法也有其局限性,比如对初始聚类中心敏感、可能陷入局部最优解等问题,因此在应用时需要仔细考虑这些因素。
二、K-均值聚类算法的基本步骤如下:
1. 初始化:随机选择K个数据点作为初始的簇中心(质心)。
2. 分配:将每个数据点分配到最近的簇中心,形成K个簇。
3. 更新:重新计算每个簇的中心,通常取簇内所有点的均值作为新的簇中心。
4. 迭代:重复步骤2和3,直到满足停止条件(如簇中心不再显著变化,或达到预设的迭代次数)。
K-均值聚类算法的优点是简单、快速,适用于处理大规模数据集。
三、局限性:
1. 对初始簇中心敏感,可能导致局部最优解。
2. 对噪声和异常值敏感。
3. 需要预先指定簇的数量K,但K的选择往往缺乏理论依据。
4. 对于非球形簇或大小不一的簇,聚类效果可能不理想。
为了解决这些问题,研究者提出了一些改进的K-均值算法,如K-中心点算法、模糊C均值算法等。同时,还可以通过特征选择、降维等预处理方法,提高K-均值聚类的性能。
四、在实际应用中面临的一些常见问题和挑战
1. **确定K值**:需要预先指定聚类的数量K,但最佳K值的确定通常缺乏理论依据,这可能影响聚类结果的质量。
2. **对初始聚类中心敏感**:算法的结果受初始聚类中心的选择影响,容易陷入局部最优解,而不是全局最优。
3. **对噪声和异常值敏感**:K-均值聚类可能无法有效处理噪声数据和异常值,这些数据点可能会对聚类中心产生较大影响,导致聚类结果不稳定。
4. **非球形聚类**:K-均值聚类假设簇是球形的,对于非球形或大小不一的簇,聚类效果可能不理想。
5. **收敛速度**:在大规模数据集上,K-均值聚类的收敛速度可能较慢。
6. **数据预处理的重要性**:K-均值聚类对特征的尺度非常敏感,因此数据的标准化或归一化处理变得尤为重要。
7. **不平衡的聚类**:K-均值聚类可能导致聚类结果不平衡,一些簇可能包含的样本量远大于其他簇。
8. **仅适用于数值型数据**:K-均值聚类主要适用于数值型数据,对于类别型特征或文本数据等非数值型数据,需要进行转换或采用其他类型的聚类算法。
9. **评估聚类效果**:缺乏一个统一的标准来评估聚类的效果,常用的评估指标如轮廓系数(Silhouette Coefficient)和误差平方和(SSE)可能无法全面反映聚类的质量。
10. **算法的稳定性**:K-均值聚类算法的迭代过程可能会因随机初始化而导致不同的结果,因此可能需要多次运行以获得最佳聚类效果。
为了解决这些问题,研究者们提出了多种改进策略,如K-Means++用于改进初始聚类中心的选择,以及使用其他聚类算法如DBSCAN或谱聚类来处理非球形数据。此外,通过特征工程、数据预处理和适当的数据转换,可以提高K-均值聚类的性能和适用性。
五、Python应用
主要得益于Python中强大的科学计算库,如NumPy和SciPy,以及专门的机器学习库,如scikit-learn。以下是K-均值聚类算法在Python中应用的一般步骤:
1. **数据准备与预处理**:在应用K-均值聚类算法之前,需要对数据进行预处理,包括清洗数据、处理缺失值、进行特征缩放等。
2. **选择K值**:确定要将数据集分成的簇的数目K。这可以通过多种方法来估计,如肘部法则(Elbow Method)、轮廓系数(Silhouette Coefficient)等。
3. **初始化质心**:随机选择K个数据点作为初始质心,或使用如K-Means++等更高级的方法来初始化质心。
4. **模型训练**:使用K-均值算法对数据进行迭代聚类。这个过程包括:
- 将每个数据点分配给最近的质心,形成簇。
- 重新计算每个簇的质心,通常是簇内所有点的均值。
5. **模型评估**:评估聚类效果,常用的评估指标包括SSE(误差平方和)、轮廓系数等。
6. **结果解释与应用**:对聚类结果进行解释,根据业务需求将聚类结果应用到实际问题中,如市场细分、推荐系统等。
7. **可视化**:使用matplotlib等库对聚类结果进行可视化,帮助理解簇的分布和特性。
在Python中,可以使用scikit-learn库中的`KMeans`类来轻松实现K-均值聚类算法。以下是一个简单的示例代码:
```python
from sklearn.cluster import KMeans
import numpy as np
from sklearn.datasets import make_blobs
# 生成模拟数据
X, y = make_blobs(n_samples=300, centers=4, cluster_std=0.60, random_state=0)
# 创建KMeans实例,设置要形成的簇数
kmeans = KMeans(n_clusters=4)
# 对数据进行拟合操作
kmeans.fit(X)
# 获取聚类标签
labels = kmeans.labels_
# 获取聚类中心
centers = kmeans.cluster_centers_
# 可视化聚类结果
import matplotlib.pyplot as plt
plt.scatter(X[:, 0], X[:, 1], c=labels, s=50, cmap='viridis')
plt.scatter(centers[:, 0], centers[:, 1], c='red', s=200, alpha=0.75)
plt.show()
```
在实际应用中,还需要考虑K-均值聚类算法的一些局限性,如对初始质心敏感、可能只能找到局部最优解等问题,并采取相应的策略来优化聚类效果。
总之,K-均值聚类算法是一种简单、有效的聚类方法,在许多领域都有广泛的应用,如市场细分、社交网络分析、图像分割等。但实际应用中需要根据具体问题,选择合适的聚类算法和参数设置。